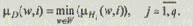Для придания общности суждениям обозначим

Тогда высказывание (4.1) можно записать в виде:




 

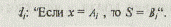
Для придания общности суждениям обозначим базовые множества U и V через W.

Тогда Аi — нечеткое подмножество W, в то время как Вi — нечеткое подмножество единичного интервала I.

Для представления правил используется операция импликации, для которой предложены различные способы нечеткой реализации.

Нечеткая импликация Лукасевича имеет вид:

 



 

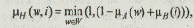
где Н — нечеткое подмножество на W ´ I,

w Î W, i Î I.

 

Аналогичным образом высказывания d1, d2,..., dq преобразуются в множества Н1, Н2, ..., Нq.

 

Их пересечением является множество D:

 

D = H1 Ç H2 Ç ... Ç Нq

 

и для каждого (w, i) Î W ´ I