семейство множеств S, состоящее из

 

Формула (5.1) читается: семейство множеств S, состоящее из всех Sj, таких, у которых элементы j принадлежат множеству J. Аналогично семейство множеств

 



 

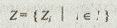
есть индексированное множество, а I — индексное множество:

 



 

Индексация позволяет различать множества, состоящие из одинаковых элементов.

Пример матрицы образов представлен в табл. 5.3.

 

Таблица 5.3 Матрица образов как семейство множеств

 

	S1	S2	S3	…	Sq
Z1	0	1	0	…	1
Z2	1	1	0	…	1
Z3	1	1	1	…	0
…	…	...	...	…	…
Zp	0	0	0	0	0

 

Семейство множеств S или Z с заданными на них отношениями можно рассматривать как системы, в которых связи между элементами образуют определенную структуру. Следовательно, содержание задач по обработке матриц образов систем включает подбор типов отношений и анализ структуры порождаемых ими систем.

Рассмотрим основные меры, порождающие отношения на множестве исследуемых систем.